Vector CANoe
The isystem.connect interface allows driving BlueBox Debuggers from almost any external application being used in the development labs. These external applications are typically test environments controlling the target microcontroller and acquiring specific data (memory content, register values, trace, profiler, code coverage) from the target microcontroller.
This document describes how to remotely drive a BlueBox from Vector CANoe Test Automation Module. As an alternative, the vTESTstudio integration is described as well.
.NET for C# test automation scenario is described.
Prerequisites
•Vector CANoe
•Vector vTESTstudio (optionally for test units)
•winIDEA
|
It is recommended to use multi-threading. CANOe is using only one single thread for simulation and testing. That means while waitUntilStop function runs, nothing in CANoe runs (e.g. event fetching from the drivers, CAPL processing, etc.) which can cause delays >1ms. |
winIDEA SDK in Test Environment
CANoe setup
|
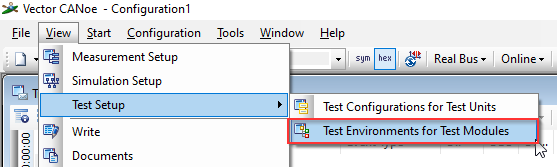
Run under View | Test setup | Test Environments for Test Modules. |
|
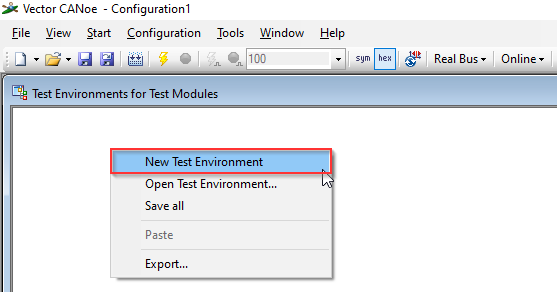
Right-click on Test Setup and select New Test Environment. |
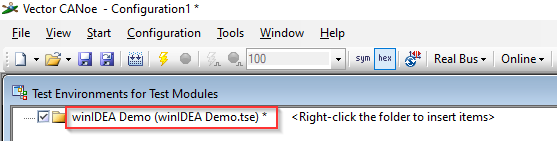
Rename the test environment and save it to disk.
 |
 |
|
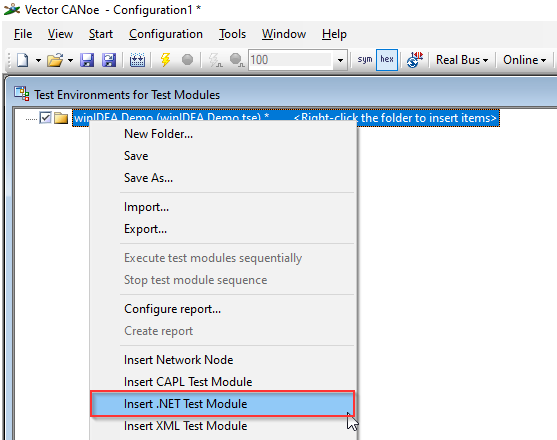
Right click the test environment and select Insert .NET test module. |
|
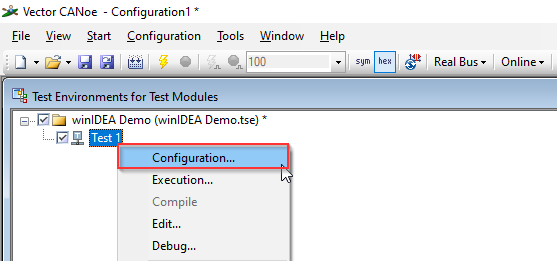
Right click the test environment and select Configuration. |
|
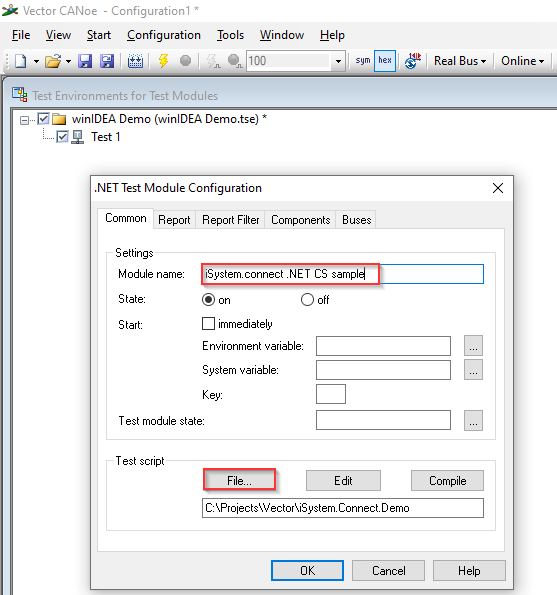
Under the Common tab rename the .NET Test Module and select the test script file (extension .cs for C#). |
|
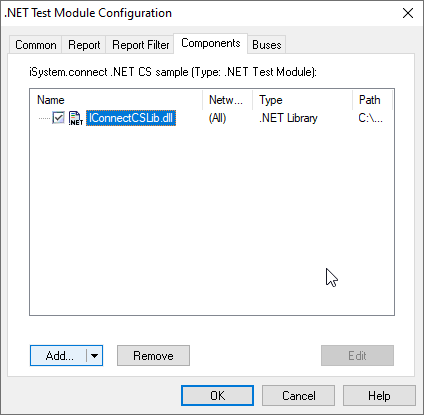
Under the Components tab register the iSYSTEM .NET library (IConnectCSLib.dll). |
This library is valid for C# .NET scripts and could be downloaded from the webpage winIDEA SDKs Download.
|
iConnectCSLib.dll and native isystemConnect.dll must be copied to CANoe executables folder location (%CANoe_home%\Exec32) or to Windows system folder. |
|
Edit and prepare .cs script. |
Refer to the downloadable Canoe configuration package iSYSTEM.Connect.Canoe.TestModulesExample.zip “iSystem.Connect.NET advanced CS sample” (file name testModules\AdvancedExample.cs), could be a good starting point for the script implementation.
|
Run the simulation and test. |
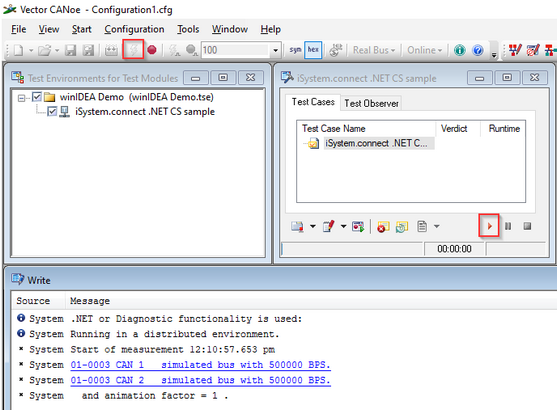
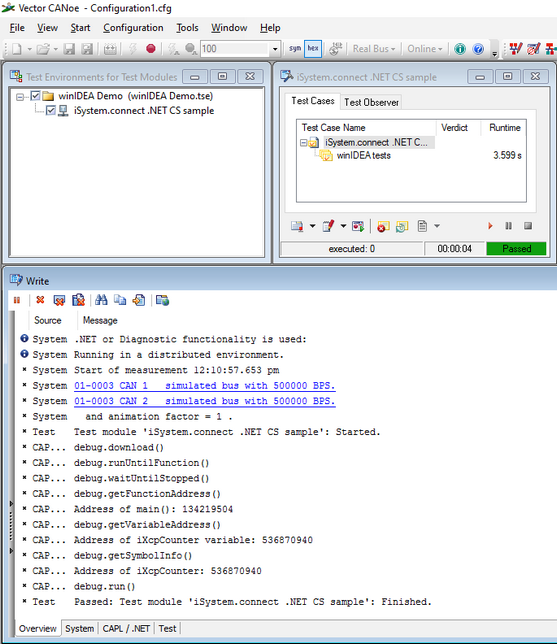
Test results are visible in the Write window.
winIDEA SDK and vTESTstudio
In vTESTstudio, you can implement tests with the help of CAPL and C# files as well as in tabular and graphic forms. In so doing, the different test languages can be easily combined. The executable entity programmed in vTESTstudio is called a test unit. It comprises all files required for the test. A test unit created in vTESTstudio has the file extension *.VTUEXE. This can be configured and executed in CANoe.
vTESTstudio setup
|
Create a new vTESTstudio project. |
|
Create a new test unit. |
|
CreateAdd a C# file to the test unit. |
|
Copy the .NET assembly iConnectCSLib.dll either to the vTESTstudio test unit folder next to the C# file or to one of its libraries. |
|
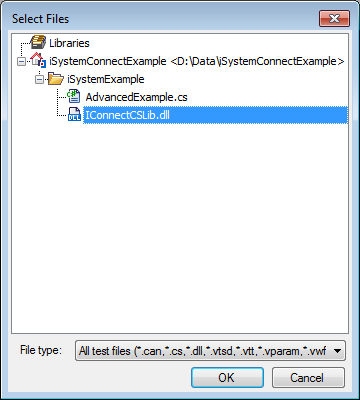
Add the .NET assembly iConnectCSLib.dll to the test unit. |
Now the the functionality of the iConnectCSLib.dll is available within the C# file.
|
Define test cases, test functions or functions within the C# file accessing the API of the iConnectCSLib.dll. |
Use the attribute [Export] to be able to call these functions in other test design languages as well, e.g. in the Test Table Editor.
|
Use the C# methods to define your test sequence - either in C# editor or in the Test Table Editor or in the Test Diagram Editor. |
|
Build the executable test unit *.VTUEXE. |
|
Vector CANoe with vTESTstudio integration sample is provided in the compressed archive iSYSTEM.Connect.Canoe.Example.Testunit.zip. |